Markov Process, Markov Reward Process

 

 

• 어제부터 구글 스터디잼이 시작했는데, 진행은 오늘부터 할 것 같다
• 가보자구!!!

 

 

---

 

 

 

 

 

Markov Process

• Markov Process란 현재 상태만 보고 미래를 결정할 수 있는 상태를 말한다
• 예를 들어 우리가 체스를 두고 있는 상황에서 중간에 내가 대신 두게 된다면 어떨까? 이전에 첫수부터 지금까지의 수까지 알 필요가 있을까? 현재 보드판의 상태만 보고도 바로 체스를 이어갈 수 있을 것이다. 이런 것을 마르코프한 상태라고 부른다.

• 위와 같은 장면의 사진만 가지고 운전을 바로 할 수 있을까? 물론 사람은 운전에 대한 사전지식을 많이 가지고 있기 때문에 할 수는 있겠지만, 현재 상태만으로는 많은 정보를 담고 있지 않기 때문에 쉽지 않을 것이다. 속력은 몇인지... 다른차가 끼어들려고 하는건지 아닌지...등
• 그럼 위와 같은 마르코프하지 않은 상태를 마르코프한 상태로 바꾸기 위해서는? 현재 시점을 t라고 할 때, t-1, t-2, t-3, t-4 이렇게 네장의 사진이 더 있다고 가정해보자.

Markov Property

• 미래는 오로지 현재 상태에만 의존하여 결정된다

아이가 잠에 드는 Markov Process

• 이 과정을 정의하는데 필요한 정보는?
  
  • 상태의 집합 𝑆 = {𝑠0, 𝑠1, 𝑠2, 𝑠3, 𝑠4}
  • 전이 확률 𝑃𝑠𝑠′

전이확률

• 𝑃𝑠𝑠′ 는 상태 s 에서 다음 상태가 s’이 될 확률
  
  • 𝑃𝑠𝑠′ = Pr[𝑠𝑡+1 = 𝑠′|𝑠𝑡 = 𝑠]
  • 예컨대 𝑃𝑠1𝑠0= 0.1, 𝑃𝑠2𝑠2 = 0
• 위와 같이 행렬 형태로 표현 가능, 전이 확률 행렬 이라고도 부른다
• MP를 정의하는데 필요한 것
  • 𝑀𝑃 ≡ {𝑆, 𝑃}

Markov Reward Process

• Markov Reward Process는 MP에서 리워드만 추가된 것이다

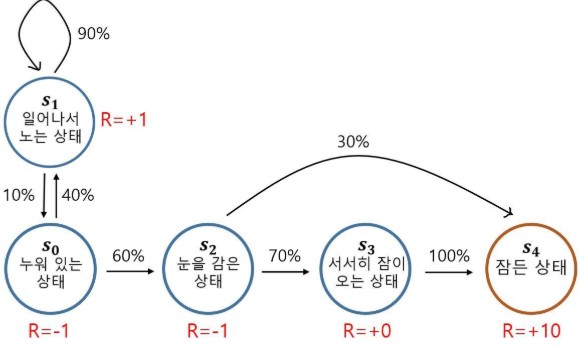
아이가 잠에 드는 Markov Reward Process

• 매 상태에 도달할때 마다 그에 걸맞는 리워드 함수가 추가되었다
• 이 과정을 정의하는데 필요한 정보는?
  
  • 상태의 집합 𝑆 = {𝑠0, 𝑠1, 𝑠2, 𝑠3, 𝑠4} -------원래 있던 애 1
  • 전이 확률 𝑃𝑠𝑠′ ---------------------------원래 있던 애 2
• 매 행동에 따라 그에 걸맞는 리워드 함수가 추가되었다
• 이 과정을 정의하는데 필요한 정보는?
  
  • 보상함수 𝑅 = 𝔼 [𝑟𝑡 | 𝑠𝑡 = 𝑠 ]------- RL에서 최적화 하고자 하는 대상
  • 감쇠 인자 γ -------------------- 0에서1 사이의 숫자

감쇠된 보상의 합, 리턴

• 사실 엄밀히 말하면 강화학습이란 리워드를 최대로 하는 것이 아닌 리턴을 최대화하는 것이다. 리턴의 기댓값을 최대화
• 리턴이란 임의의 시점 t에서 미래에 받을 리워드의 합이다
  • 𝐺𝑡 = 𝑟𝑡+1 + 𝑟𝑡+2 + 𝑟𝑡+3 + 𝑟𝑡+4 + ⋯
• 이때 미래 시점을 감쇠한다
  • $𝐺𝑡 = 𝑟𝑡+1 + γ𝑟𝑡+2 + γ^{2}𝑟𝑡+3 + γ^{3}𝑟𝑡+4 + ⋯$
• 리턴은 어떤 상태의 value를 측정하는데 중요한 의미를 가진다

감쇠 인자 γ 는 왜 필요할까?

1. 수학적 편리성
   • 감쇠 인자가 없다면 무한대와 무한대를 비교하는 경우가 생기게 되기 때문에 수학적으로 증명을 할 때 힘든 경우가 생김
2. 사람의 선호(미래에 대한 불확실성) 반영
   • 미래에는 어떻게 될지 모르니 현재가 더 중요

• 감쇠 인자가 0이면 현재 시점을 더 중요시하는 것을 의미
• 감쇠 인자가 1이면 미래 지향적이라고 볼 수 있음

MRP를 정의하는 데 필요한 것

• 𝑀𝑅𝑃 ≡ {𝑆, 𝑃, 𝑅, 𝛾}

 

 

 

 

---