사이킷런 개요, 가상 데이터, 데이터 분할, ROC 커브

 

 

• 어제 천재 혁명가 곽상빈이라는 유튜브에서 나만의 부적만들기라는 컨텐츠를 보고 따라해보려고 하는 중이다
• 10년 후의 나의 모습, 5년 후, 3년 후를 생각해서 작성하려다 보니 쉽지 않다
• 항상 계획을 짜야지 짜야지 생각은 했었는데 막상 해보려고 하니 어렵다
• 매달, 매주, 매일 계획을 짜고 하나씩 달성해보자

 

 

 

 

---

 

 

 

 

 

 

1. 사이킷런(Scikit-Learn) 개요

• 사이킷런(scikit-learn)은 기계 학습을 위한 다양한 기능을 제공하는 파이썬 라이브러리다
  
  • 가상 데이터(분류 등) 생성 기능을 제공한다
  • 기계 학습을 위해 다양한 기본적인 데이터 세트를 제공한다
  • 다양한 기계 학습 모델(SVM, 랜덤 포레스트 등)을 제공한다

1-1. 사이킷런에서 제공하는 데이터 세트 예시 - 붓꽃(iris) 품종 예측 데이터 세트

• 붓꽃에 대한 정보가 주어지면, 어떠한 붓꽃 클래스에 해당하는지 맞히는 데이터 세트다
  • 총 150개의 데이터로 구성된다

• 대표적인 지도 학습 데이터다
  
  • 지도 학습(Supervised Learning)이란 데이터에 대하여 정답 레이블(label)이 존재하는 상황에서의 학습 방법이다
  • 지도 학습의 전형적인 예시는 다음과 같다
    
    • 학습 단계: 이미지  x 를 보고 레이블  y 를 예측하도록 학습
    • 테스트 단계: 새로운 이미지  x 가 주어졌을 때, 클래스를 예측하기
• 입력 데이터는 4개의 특징으로 구성된다
  
  • 꽃받침 길이(sepal length)
  • 꽃받침 너비(sepal width)
  • 꽃잎 길이(petal length)
  • 꽃잎 너비(petal width)
• 출력 데이터는 3개의 클래스로 구성된다
  
  • 부채붓꽃(setosa)
  • 버시컬러(versicolor)
  • 버지니카(virginica)

from sklearn.datasets import load_iris

# 데이터 세트 불러오기
dataset = load_iris()
# 데이터 세트에서 필요한 정보 가져오기
data = dataset["data"]
target = dataset["target"]
feature_names = dataset["feature_names"]
target_names = dataset["target_names"]

print(f"총 데이터 개수: {len(data)}")
print("[입력 특징]")
for i in range(len(feature_names)):
    feature_name = feature_names[i]
    print(f"{i + 1}: {feature_name}")
print("[입력 데이터 예시]")
print(data[:5])
print("[출력 특징]")
for i in range(len(target_names)):
    target_name = target_names[i]
    print(f"{i + 1}: {target_name}")
print("[출력 데이터 예시]")
print(target[:5])

2. 사이킷런(Scikit-Learn) 가상 데이터 생성

• 사이킷런은 가상 데이터(분류 등) 생성 기능을 제공한다
• 분류(classification) 모델 학습을 위한 가상 데이터 생성을 진행할 수 있다

import pandas as pd
import matplotlib.pyplot as plt

plt.rcParams["figure.figsize"] = [10, 8]

2-1. make_blobs

• 정규 분포를 따르는 가상의 데이터를 생성한다
• 여러 개의 클러스터가 존재하는 형태로 데이터가 생성된다
• 파라미터 설명
  
  • n_samples: 생성할 데이터의 개수 (default: 100)
  • centers: 생성할 클러스터의 수 (default: 3)
  • n_features: 입력 차원 (default: 2)
  • cluster_std: 클러스터의 표준 편차 (default: 1.0)
  • random_state: 랜덤 데이터 생성 시드(seed)
  • return_centers: 클러스터의 중심(center) 값을 반환할지 여부 (default: False)

from sklearn.datasets import make_blobs

# 2D data with 3 classes.
X, y = make_blobs(n_samples=100, centers=3, n_features=2, random_state=1234)
df = pd.DataFrame(dict(x=X[:,0], y=X[:,1], label=y))
print(df.head())

print("데이터의 개수:", len(df))
print(df["x"].head()) # 데이터 x
print(df["y"].head()) # 데이터 y

plt.scatter(df["x"], df["y"], s=100, c=y)
plt.xlabel("$X_1$")
plt.ylabel("$X_2$")
plt.show()

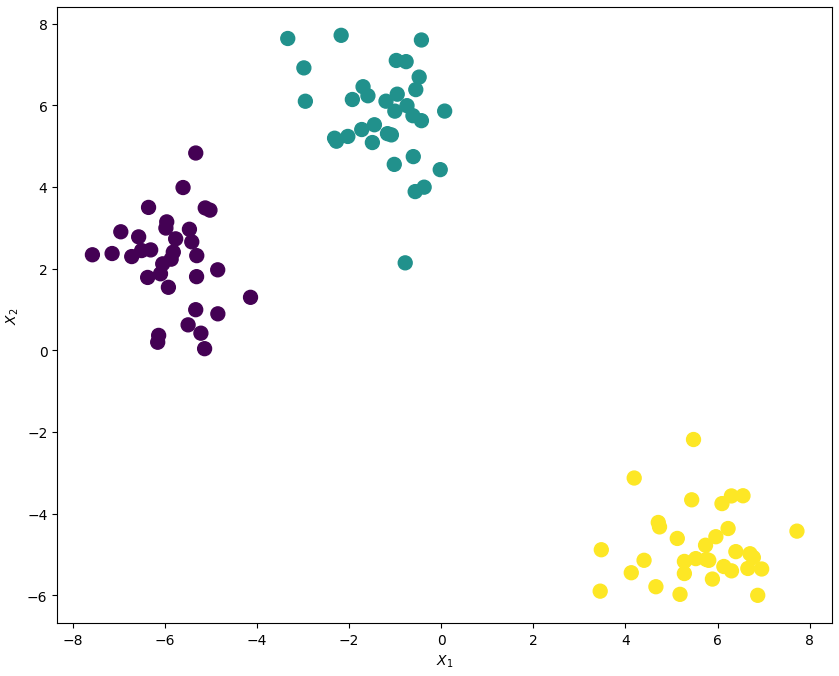
2-2. make_moons

• 초승달 모양의 클러스터 두 개를 생성한다
• 주로 비선형 분류 모델을 평가하기 위한 목적으로 사용된다
• 파라미터 설명
  
  • n_samples: 생성할 데이터의 개수
  • noise: 데이터 노이즈 크기로, noise가 클수록 아웃라이어가 생성된다
    → noise가 0일 때는 정확히 구분되는 두 개의 초승달 형태를 띤다
  • random_state: 랜덤 데이터 생성 시드(seed)

from sklearn.datasets import make_moons

# noise가 0일 때는 정확히 구분되는 달(moon)의 모양, noise가 클수록 아웃라이어 생성
X, y = make_moons(n_samples=500, noise=0.05, random_state=1234)
df = pd.DataFrame(dict(x=X[:,0], y=X[:,1], label=y))
print(df.head())

print("데이터의 개수:", len(df))
print(df["x"].head()) # 데이터 x
print(df["y"].head()) # 데이터 y

plt.scatter(df["x"], df["y"], s=100, c=y)
plt.xlabel("$X_1$")
plt.ylabel("$X_2$")
plt.show()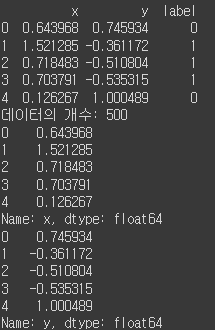

2-3. make_circles

• 하나의 작은 원을 포함하는 큰 원을 생성한다
• 클러스터링 혹은 분류 알고리즘을 평가하기 위한 목적으로 사용된다
• 파라미터 설명
  
  • n_samples: 생성할 데이터 개수
  • noise: 데이터 노이즈 크기로, noise가 클수록 아웃라이어 생성된다
    → noise가 0일 때는 정확히 구분되는 두 개의 원(circle) 형태를 띤다
  • random_state: 랜덤 데이터 생성 시드(seed)

from sklearn.datasets import make_circles

# noise가 0일 때는 정확히 구분되는 원(circle)의 모양, noise가 클수록 아웃라이어 생성
X, y = make_circles(n_samples=500, noise=0.05, random_state=1234)
df = pd.DataFrame(dict(x=X[:,0], y=X[:,1], label=y))
print(df.head())

print("데이터의 개수:", len(df))
print(df["x"].head()) # 데이터 x
print(df["y"].head()) # 데이터 y

plt.scatter(df["x"], df["y"], s=100, c=y)
plt.xlabel("$X_1$")
plt.ylabel("$X_2$")
plt.show()

2-4. make_regression

• 회귀 문제(regression problem)를 위한 가상 데이터를 생성한다
• 직선 형태의 분포를 가지는 데이터가 생성된다
• 파라미터 설명
  
  • n_samples: 생성할 데이터 개수 (default: 100)
  • n_features: 입력 차원 (default: 100)
  • n_targets: 출력 차원 (default: 1)
  • noise: 데이터 노이즈 크기로, noise가 클수록 아웃라이어 생성된다.
  • random_state: 랜덤 데이터 생성 시드(seed)

from sklearn.datasets import make_regression

X, y = make_regression(n_samples=500, noise=5, n_features=1, random_state=1234)
df = pd.DataFrame(dict(x=X[:,0], y=y))
print(df.head())

print("데이터의 개수:", len(df))
print(df["x"].head()) # 데이터 x
print(df["y"].head()) # 데이터 y

plt.scatter(df["x"], df["y"], s=100, c=y)
plt.xlabel("$X$")
plt.ylabel("$Y$")
plt.show()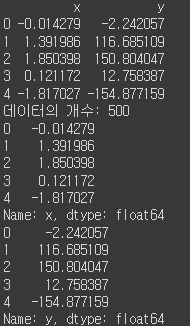

3. 사이킷런(Scikit-Learn) 학습 데이터와 테스트 데이터 분할

3-1. 오버피팅(Overfitting)

• 우리는 학습 데이터(training data)에서 매우 높은 성능을 보이는 딥러닝 모델을 만들 수 있다
• 하지만, 실질적으로 테스트 단계에서는 좋은 정확도를 얻지 못하는 경우가 많다
• 학습 데이터에만 과도하게 맞추어져서 그 외의 것에서는 좋지 못한 정확도를 보여주는 것을 오버피팅이라고 부른다

3-2. 검증 데이터 세트

• 오버피팅을 해결하기 위해서 검증 절차와 테스트 절차를 추가한다
• 학습(training) 데이터 세트를 이용해서 학습을 진행하되, 별도의 검증 데이터 세트에 대해서 가장 정확도가 높을 때의 모델을 저장한다
• 검증 정확도가 제일 높은 모델을 최종적으로 사용한다
• 보통 데이터 세트를 다음과 같이 구성한다
  학습 데이터 세트 / 검증 데이터 세트 / 테스트 데이터 세트

3-3. 데이터 세트의 구분

• 학습 데이터 세트
  
  • 모델을 실질적으로 학습하기 위해 사용하는 데이터 세트다
  • 일반적으로 전체 데이터 세트에서 60%~80% 정도를 학습 데이터 세트로 사용한다
• 검증 데이터 세트
  
  • 학습된 모델을 검증(validation)하기 위해 사용하는 데이터 세트다
  • 검증용 데이터에 대하여 높은 성능이 나오는 것이 목적이다
  • 네트워크의 하이퍼 파라미터를 조절하여 검증용 데이터에 높은 성능이 나오도록 한다
• 테스트 데이터 세트
  
  • 학습된 모델을 최종적으로 테스트하기 위해 사용하는 데이터 세트다
  • 학습된 모델이 과대적합(overfitting)되어 학습용/검증용 데이터에 대해서만 잘 동작하는 경우가 있다
  • 테스트 데이터를 이용해 모델에 대하여 최종적으로 성능 평가를 진행할 수 있다

3-4. 학습 데이터와 테스트 데이터 분할

• 사이킷런(scikit-learn) 라이브러리는 학습/테스트 데이터 분할 기능을 제공한다
• train_test_split() 함수를 사용할 수 있다
• 파라미터
  
  • arrays: 분할시킬 데이터(python list, NumPy array, pandas dataframe 등)
  • test_size: 테스트 데이터 세트의 비율 (default: 0.25)
  • shuffle: 데이터 섞기 여부 (default: True)
  • random_state: 랜덤 시드(seed) / 학습 데이터를 랜덤으로 생성
• 반환(return)
  
  • (X_train, X_test): 레이블 없이 데이터만 넣었을 때
  • (X_train, X_test, Y_train, Y_test): 데이터와 레이블을 모두 넣었을 때

train_test_split(X, Y, test_size=0.2)

 

3-4-1. 간단한 데이터 세트를 만들어 분할해보기

from sklearn.model_selection import train_test_split

X = [
    [0, 1, 2, 3],
    [2, 3, 1, 4],
    [5, 2, 3, 5],
    [3, 5, 2, 1],
    [7, 5, 3, 5]
]
Y = [0, 0, 1, 2, 0]

# 데이터(X)만 입력한 경우
X_train, X_test = train_test_split(X, test_size=0.2, random_state=7777)
print(f"X_train: {X_train}")
print(f"X_test: {X_test}")

# 데이터(X)와 레이블(Y)을 모두 넣은 경우
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.4, random_state=7777)
print(f"X_train: {X_train}")
print(f"X_test: {X_test}")
print(f"Y_train: {Y_train}")
print(f"Y_test: {Y_test}")

• 앞서 보았던 iris 데이터 세트에 대하여 분할해보기

from sklearn.datasets import load_iris

# 데이터 세트 불러오기
dataset = load_iris()
# 데이터 세트에서 필요한 정보 가져오기
data = dataset["data"]
target = dataset["target"]
feature_names = dataset["feature_names"]
target_names = dataset["target_names"]

print(f"총 데이터 개수: {len(data)}")
print("[입력 특징]")
for i in range(len(feature_names)):
    feature_name = feature_names[i]
    print(f"{i + 1}: {feature_name}")
print("[입력 데이터 예시]")
print(data[:5])
print("[출력 특징]")
for i in range(len(target_names)):
    target_name = target_names[i]
    print(f"{i + 1}: {target_name}")
print("[출력 데이터 예시]")
print(target[:5])

from sklearn.model_selection import train_test_split

X_train, X_test, Y_train, Y_test = train_test_split(
    data,
    target,
    test_size=0.2,
    random_state=2000
)
print(f"학습 데이터 개수: {len(X_train)}")
print(f"테스트 데이터 개수: {len(X_test)}")

# 학습 데이터의 입력 특징(features) 출력
df = pd.DataFrame(X_train, columns=feature_names)
print(df)

# 학습 데이터의 정답 레이블 카테고리(category) 출력
series = pd.Series(Y_train, dtype="category")
series = series.cat.rename_categories(target_names)
print(series)

# 테스트 데이터의 입력 특징 출력
df = pd.DataFrame(X_test, columns=feature_names)
print(df)

# 테스트 데이터의 정답 레이블 출력
series = pd.Series(Y_test, dtype="category")
series = series.cat.rename_categories(target_names)
print(series)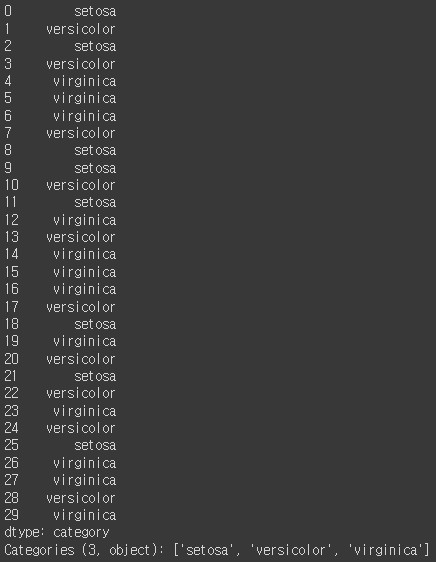

4. 사이킷런(Scikit-Learn) ROC 커브(Curve)

• 분류 모델이 얼마나 기능을 잘 수행하는지 판단하기 위해서 기준이 필요한데 이 때 ROC 커브를 사용할 수 있다
• TP (True Positive) : 올바르게 "양성"이라고 판단
• FP (False Positive) : 실수로 "양성"이라고 판단 (정답은 "음성")
• TN (True Negative) : 올바르게 "음성"이라고 판단
• FN (False Negative) : 실수로 "음성"이라고 판단 (정답은 "양성")
• 민감도(Sensitivity)와 특이도(Specificity)
  • 민감도(Sensitivity) = TPR (True Positive Rate) = TP / (TP + FN)
    실제로 양성인 것들에 대하여 양성 판정을 정확히 하는지를 의미한다
    높을수록 좋다
  • 특이도(Specificity) = TNR (True Negative Rate) = TN / (TN + FP)
    실제로 음성인 것들에 대하여 음성 판정을 정확히 하는지를 의미한다
    높을수록 좋다

4-1. ROC Curve

• ROC (Receiver Operating Characteristic) 곡선(curve)라는 의미를 가진다
• 사용할 수 있는 모든 threshold에 대하여 TPR과 FPR을 나타낸 것이다
• TPR (True Positive Rate) = Recall = Sensitivity = TP / (TP + FN)
  → (정답을 맞힌 비율이므로) 높을수록 좋다
• FPR (False Positive Rate) = (1 - Specififcity) = FP / (TN + FP)
  → (정답을 맞히지 못한 비율이므로) 낮을수록 좋다
• TPR이 높을수록, FPR도 높아지는 경향이 있다

• threshold가 0.5일 때
  
  • 0.5 이상인 경우, 전부 양성(positive)이라고 판단한다
  • 모든 positive를 양성으로 정확히 판단한다
  • TP = 6, FP = 4, TN = 10, FN = 0 (합계는 20)
  • 따라서 TPR = 1 (100%), FPR = 4 / 14 (28.6%)
• threshold가 0.8일 때
  
  • 0.8 이상인 경우, 전부 양성(positive)이라고 판단한다
  • 모든 negative를 음성으로 정확히 판단한다
  • TP = 4, FP = 0, TN = 14, FN = 2 (합계는 20)
  • 따라서 TPR = 4 / 6 (66.6%), FPR = 0 (0%)
• threshold를 바꾸어 가며 (TPR, FPR)을 한 점(point)으로 간주하고, 각 점을 찍어서 그래프로 표현할 수 있다

4-2. AUC (Area Under Curve)

• 곡선(curve)의 아래쪽에 해당하는 면적(area)을 의미한다
• AUROC (Area Under ROC)라고 부르기도 한다
• sklearn의 roc_auc_score 메서드를 사용할 수 있다
• 기본적으로 y_real의 값은 0 (음성), 1 (양성)의 값을 사용한다

from sklearn.metrics import roc_auc_score

# 모델의 예측(prediction)
y_pred = [
    0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45,
    0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95
]
# 정답 레이블(real label)
y_real = [
    0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
    1, 0, 0, 1, 0, 0, 1, 1, 1, 1
]

score = roc_auc_score(y_real, y_pred)
print(f"AUROC score: {score:.6f}")

4-3. AUC 직접 계산해보기

• confusion_matrix() 메서드는 정답(real)과 에측 결과(prediction)가 주어졌을 때 TN, FP, FN, TP를 반환한다

from sklearn.metrics import confusion_matrix

def get_tpr_fpr(y_real, y_pred):
    cm = confusion_matrix(y_real, y_pred)
    TN = cm[0, 0]
    FP = cm[0, 1]
    FN = cm[1, 0]
    TP = cm[1, 1]
    # TPR과 FPR 계산
    TPR = TP / (TP + FN) # TPR (Sensitivity)
    FPR = FP / (TN + FP) # FPR (1 - Specificity)
    return TPR, FPR

import numpy as np

y_prob = np.asarray([
    0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45,
    0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95
])
y_real = np.asarray([
    0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
    1, 0, 0, 1, 0, 0, 1, 1, 1, 1
])

threshold = 0.5
y_pred = y_prob >= threshold
TPR, FPR = get_tpr_fpr(y_real, y_pred)
print(y_pred)
print(f"TPR: {TPR * 100.:.4f}%")
print(f"FPR: {FPR * 100.:.4f}%")

• threshold를 바꾸어 가며 (TPR, FPR)을 한 점(point)으로 간주하고, 각 점을 찍어서 그래프로 표현한 후에 (TPR, FPR) 점들이 차지하는 아래 면적(area)을 계산하면 이것이 AUC이다

def get_n_points(y_real, y_prob, n):
    # 전체 예측 결과를 정렬한 뒤에 고유한(unique) 원소만 추출
    sorted_pred = np.unique(np.sort(y_prob))

    # 예측 결과의 개수
    length = len(sorted_pred)
    n = min(length, n)
    step = length / n

    # 최종적으로 선택된 N개의 인덱스(index) 리스트
    indices = []
    current = 0
    for i in range(n):
        index = int(current)
        indices.append(index)
        current += step

    # 기본적으로 (FPR=0, TPR=0) 포인트가 존재
    points = [(0.0, 0.0)]
    for index in indices:
        # 최대 N개의 균등하게 얻은 threshold에 대하여 TPR, FPR 계산
        threshold = y_prob[index]
        y_pred = y_prob >= threshold
        TPR, FPR = get_tpr_fpr(y_real, y_pred)
        # 저장할 때는 (x축: FPR, y축: TPR) 형태로 저장
        points.append((FPR, TPR))

    return points


points = get_n_points(y_real, y_prob, 30)
print(points)

# [(0.0, 0.0), (1.0, 1.0), (0.9285714285714286, 1.0), (0.8571428571428571, 1.0), (0.7857142857142857, 1.0), (0.7142857142857143, 1.0), (0.6428571428571429, 1.0), (0.5714285714285714, 1.0), (0.5, 1.0), (0.42857142857142855, 1.0), (0.35714285714285715, 1.0), (0.2857142857142857, 1.0), (0.2857142857142857, 0.8333333333333334), (0.21428571428571427, 0.8333333333333334), (0.14285714285714285, 0.8333333333333334), (0.14285714285714285, 0.6666666666666666), (0.07142857142857142, 0.6666666666666666), (0.0, 0.6666666666666666), (0.0, 0.5), (0.0, 0.3333333333333333), (0.0, 0.16666666666666666)]

import seaborn as sns

def plot_roc_curve(points):
    # (x축: FPR, y축: TPR)에 대하여 오름차순 정렬
    points = sorted(points)
    plt.plot([point[0] for point in points], [point[1] for point in points], color="red")
    sns.lineplot(x=[0,1], y=[0,1], color="green")
    plt.show()

def get_auroc(points):
    # (x축: FPR, y축: TPR)에 대하여 오름차순 정렬
    points = sorted(points)

    # 곡선(curve)은 항상 비내림차순 형태를 보인다.
    area = 0
    cur_x = 0.0
    cur_y = 0.0
    for point in points:
        x, y = point
        if cur_x == x:
            cur_y = y
        else:
            area += (x - cur_x) * cur_y
            cur_x = x
            cur_y = y
    return area

plot_roc_curve(points)
area = get_auroc(points)
print(f"AUROC score: {area:.6f}")

 

 

 

 

 

 

 

---