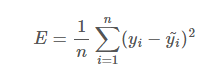선형 회귀, 경사 하강법, 가중치 초기화, SGD

 

 

• 유튜브에서 "이해라는 것은 뒤늦게 찾아온다" 라는 말을 들은 적이 있다
• 확실히 처음 들었을 때는 잘 몰랐던 것들이 계속 공부를 하다보니 조금씩 이해가 되는 부분이 많은 것 같다
• 그러니까 이해 안돼도 닥치고 그냥 하자

진행시켜

 

 

 

 

 

 

 

---

 

 

 

 

 

 

1. 선형 회귀 (Linear Regression)

• 선형 회귀란 입력과 출력 간의 (선형적인 데이터에서) 관계를 파악하여 처음 보는 입력에 대해서도 적합한 출력을 얻는 것
• 예를 들어 키와 몸무게의 선형적인 관계를 파악해서 데이터에 없는 키가 주어졌을 때에도 적합한 몸무게를 예측할 수 있다
• 즉, f(x)=ax+b에서 적절한 a와 b를 찾는 것이 목표인데 어떻게? 어떤 기준으로? 찾을 수 있을까?
• 바로 loss(또는 cost)를 최소화하는 a와 b를 찾는 것이 최종 목표가 되겠다
• Loss 함수에도 종류가 다양하게 있는데 그 중에 MSE (Mean Squared Error)를 사용해보자

MSE 수식

• MSE는 문자 그대로 오차를 제곱한 값의 평균을 Loss로 두고 이 Loss 값을 최대한 줄이는 것을 목표로 하는 겁니다
• 이 Loss를 최소로 하는 a와 b를 찾기 위해서 a,b 값을 하나 하나 바꿔가면 L 값을 그래프로 그려서 최솟값을 찾는다?
• 물론 가능은 하지만...
• 너무 비효율적이다

• 대충 이런 모양의 그래프가 나올 것이다 (x축은 a, y축은 b, z축은 Loss)
• 참고로 선형회귀에서 Loss 값은 0일 수가 없다
• 왜냐하면 Loss가 0이라는 것은 모든 데이터를 그대로 따른 다는 것인데 그렇다면 그래프가 직선이 될 수 없고 지그재그 모양처럼 되기 때문이다

• 여튼 다시 본론으로 돌아와서 이렇게 하나씩 a와 b를 대입해서 그래프를 그리지 싫어서 나온 것이 경사 하강법이다

2. 경사 하강법 (Gradient Descent)

• 그라디언트란 편미분을 열벡터로 표현한 것이다
• 어떠한 a와 b에서 그라디언트 값을 구하면 항상 그 값은 가파른 방향을 향하게 되는 그라디언트의 특징을 이용한 것이다
• 왜 항상 가장 가파른 방향을 향하는지는 따로 포스팅하여 정리하겠다
• 여튼 항상 가파른 방향을 향하니까 우리가 원하는 Loss 값이 가장 작을 때, 즉 기울기가 0에 수렴할 때는 그라디언트의 반대 방향으로 이동하면 되는 것이다!!!
• 즉, 어떠한 a와 b를 임의로 정하고 그라디언트를 구한 후에 반대 방향으로 a와 b를 옮기다 보면 Loss가 최소가 되는 값을 구할 수 있다는 것이다

신기하죠?

• 하지만 그라디언트를 그대로 이용하게 되면 문제가 생길 수 있다
• 간단하게 $y=x^{2}$ 그래프를 보고 왜 그런지 살펴보자

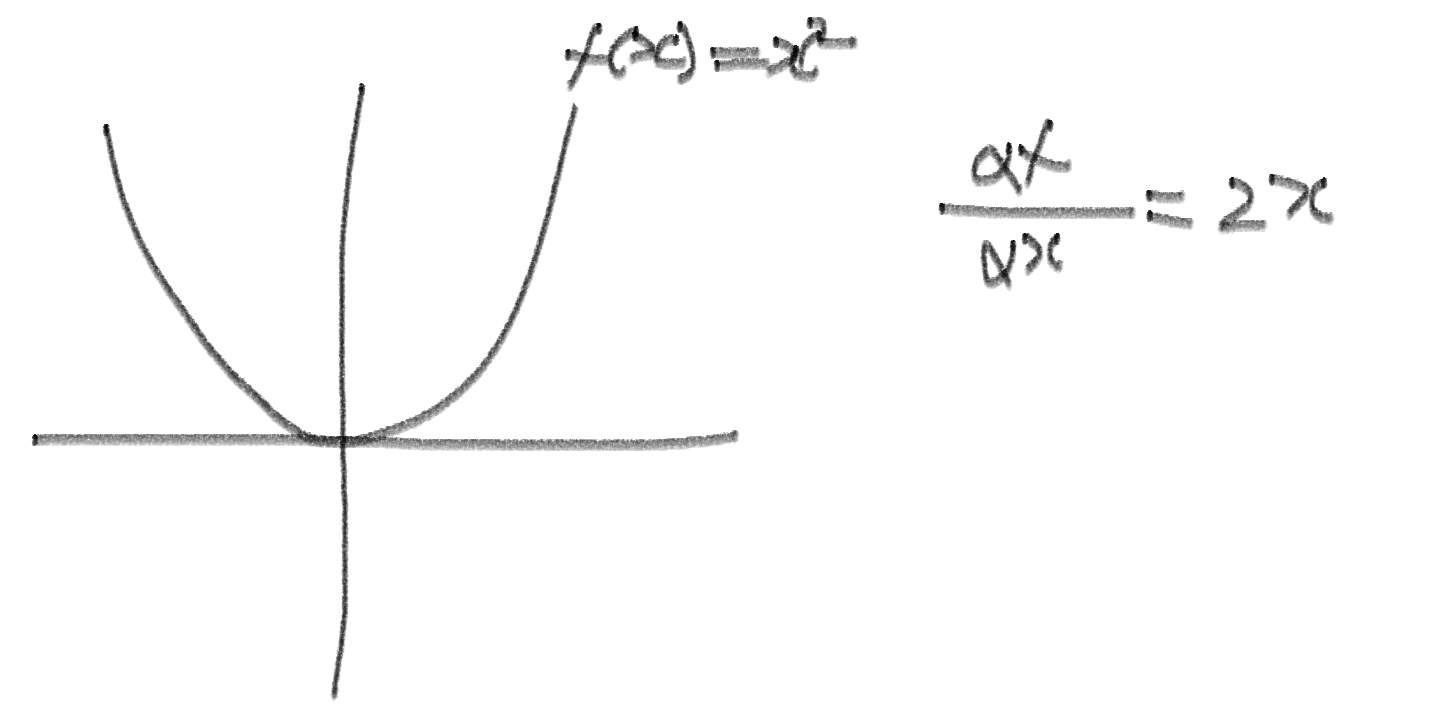
• 여기서 x가 1일 때 미분값은 2이고, 반대로 가야하므로 1에서 2를 빼주면 -1로 간다
• 그리고 이것의 미분값은 -2이고 반대로 가야하므로 -1 에서 -2를 빼주면 1로 간다
• 이렇게 무한 반복;;;
• 이렇게 미분값이 생각보다 클 수도 있다는 점을 고려하지 않으면 우리가 원하는 Loss를 최소로 하는 a와 b 값을 그냥 지나쳐버릴 수도 있다는 것이다
• 그래서 이것을 해결하기 위해서 Learning rate $\alpha$ (보폭)를 곱해준다
• 러닝 레이트를 0.1로 주었다고 하였을 때, x가 1이면 미분값 2에서 0.1를 곱한 값을 반대로 가게 해주면 1 - (2 * 0.1) = 0.8로 가게 되고, 0.8에서 다시 미분하고 그 값에 러닝 레이트를 곱해서 반대로 보내주고를 반복하게 된다
• 러닝 레이트 값은 상수로 두기도 하고 러닝 레이트 스케줄링 알고리즘에 의해서 변화를 주면서 계산을 하기도 한다
• 러닝 레이트를 상수값으로 두어도 Loss를 최소로 하는 값 a와b를 지나치지 않고 찾을 수 있는 이유는 기울기(미분값)를 계속 줄여가면서 계산하니까 결국에는 0에 수렴하게 되어서 Loss를 최소로 하는 값 a와 b에 수렴하게 되는 것이다 👍

알파는 러닝 레이트를 의미함

2-1. 경사 하강법 (Gradient Descent)의 문제점 

1. 일단 모든 데이터 값들을 참조해서 식을 계산해야 하기 때문에 느리다...
2. local minimum에 빠질 수 있다. 그라디언트라의 특징 자체가 주변에 가장 가까운 곳의 가파른 방향으로 향하기 때문에 그래프가 $y=x^{2}$처럼 간단하지 않고 울퉁불퉁할 경우에 잘못하면 이상한 곳으로 향할 수 있다

• 그래서 맨처음 임의의 a와 b를 고를 때 아무곳이나 고르면 안된다
• a와 b, 즉, 가중치를 처음에 선택하는 방법(초기화)에 대해서 알아보자

3. 가중치 초기화 (Weight Initializaion)

• 크게 3가지가 있다
• 각 방법마다 적합한 Activation이 따로 있다 (Unit Step Function, Sigmoid, ReLU 등)
• He가 발표한 방식을 대체로 많이 사용한다

4. SGD (Stochastic Gradient Descent)

• 그라디언트에서 연산 속도를 빠르게 하기 위해서 매번 모든 데이터들을 참조해서 계산하는 것이 아니라 랜덤하게 데이터를 하나씩 뽑아서 계산하는 방식을 말한다 (균등 분포하게)
• 비복원 추출 방식을 사용하기 때문에 5개의 데이터 중 첫번째를 뽑았다면 뽑은 데이터를 제외하고 나머지 4개에서 다시 랜덤하게 뽑고 진행하는 식으로 한다
• 다 뽑고 나면 다시 모든 데이터를 넣고 거기서 다시 비복원 추출을 진행하면서 Loss에 수렴하는 a와 b를 얻을 때까지 반복한다
• 하지만 전체 값들을 보고 그라디언트 값을 결정하는 것이 아니기 때문에 그래프의 모양이 매우 변칙적으로 변화하게 된다
• 그렇기 때문에 local minimum을 탈출할 수 있을 수도 있다 (운이 좋으면) 하지만 완벽한 예방 방법은 아니다

5. mini-batch SGD

• SGD는 하나씩 보았다면 mini-batch SGD는 배치 사이즈를 정해서 계산을 진행한다. GPU 특성상 여러 데이터를 병렬로 계산할 수 있기 때문에 속도적인 측면에서도 빠르다고 볼 수 있다(GPU가 허락하는 한 최대한 키우는 것이 좋음)
• batch size란 5개의 데이터에서 배치 사이즈를 2로 정할 경우 비복원 추출 방식으로 랜덤하게 2개를 뽑고 나머지 3개에서 2개 뽑고 마지막에서는 하나 남은 것만 뽑는 것이다. 그리고 Loss에 수렴하는 a와 b를 얻을 때까지 반복한다
• 그리고 배치 사이즈를 키울 경우, 러닝 레이트를 같이 키워야 한다는 연구 결과가 있으므로 참고하자
• Weight 값처럼 AI가 알아서 구해내는 것이 아니라 직접 넣어주어야 하는 것들을 HyperParameter라고 부른다
  • 총 Epoch 수
  • Batch Size
  • Learning Rate
  • Model Architecture

 

 

 

 

 

 

 

 

 

---