Momentum, Adam, Validation, DNN

 

 

• 앞부분 강의는 들으면서 나중에 이해될거야! 하면서 일단 받아들이는 느낌으로 갔었는데 혁펜하임 성님 강의는 기초부터 찬찬히 설명해주셔서 이해가 쏙쏙되니까 들을 맛이 난다!!! (물론 이해 안되는 부분도 있긴 함ㅎ)
• 언젠가 인공지능 박사까지 취득하는 그 날을 상상하며 오늘도 달려보자~!

 

 

 

 

 

 

 

---

 

 

 

 

 

0. Optimizer

• Optimizer는 딥러닝에서 Network가 빠르고 정확하게 학습하는 것을 목표로 한다 
• 밑에 그림들은 포스팅 전체를 읽고 다시 훑어보면 좋을 것 같다
  

  

 

다양한 Optimizer

1. Momentum vs RMSProp (Root Mean Square Propagation)

1-1. Momentum

• 모멘텀이랑 관성, 탄성, 가속도를 의미하는 단어이다
• 즉, SGD처럼 휙휙 꺾이지 말고 이전의 그라디언트를 계속 고려해주며 마치 관성에 의해 가던 방향을 잊지 못하고 덜 꺾이는 것처럼 만들어주자는 것이다

• 즉, 방향을 컨트롤해줘서 최적화를 시켜주는 것이다
• Momentum은 빠른학습속도와 local minima를 문제를 개선하고자 SGD에 관성의 개념을 적용
• 일반적으로 관성계수 m은 0.9를 사용

1-2. RMSProp

• 모멘텀이 방향을 컨트롤해주었다면 RMSProp은 스텝의 보폭을 컨트롤하여 최적화하는 기법이다
• 공평하게 탐색할 수 있도록 많이 훑은 축으로는 적게, 적게 훑은 축으로는 많이 탐색하여 평준화를 시켜준다

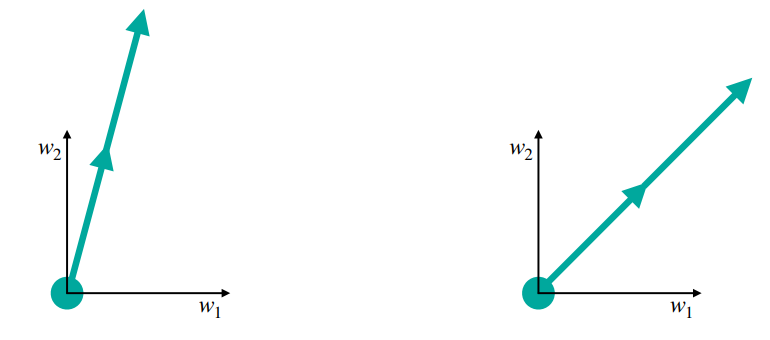
• 모멘텀처럼 이전의 크기를 잊지 않고 계속 고려해주면서 많이 훑은 축으로는 적게, 적게 훑은 축으로는 많이 탐색

2. Adam (Adaptive Moment Estimation)

• RMSProp와 Momentum 기법을 합친 Optimizer이다

출처 : https://arxiv.org/pdf/1412.6980.pdf

• 앞에서 보았던 그라디언트 수식과 저 부분만 다르니 V랑 m이 무엇인지만 확인해보자
• $t \leftarrow 0$이므로 t가 0일 때부터 하나씩 살펴보자
• $\beta$는 0과 1사이의 값이므로 원래는 0.9 이런식으로 잡아야 하지만 계산하기 쉽게 $\frac{1}{2}$로 두고 살펴봅시다

• 이런식으로 이전의 그라디언트 값을 고려하긴 하는데 점점 잊혀져간다
  → 이런걸 지수이동평균 (Exponential Moving Average) 이라고 부른다
• 그리고 v는 m에서 $\beta_{1}$과 $\beta_{2}$의 위치만 서로 바뀌고 $g_{t}$가 $g^{2}_{t}$로 바뀌기만 하고 나머지는 같다

• 이렇게 구해진 m과 v로 $\theta_{t} \leftarrow \theta_{t-1} - \alpha \frac{m_{t}}{\sqrt V_{t}}$ 를 구해주면 된다
• 참고로 v에서 벡터의 제곱은 각 요소들을 제곱해주면 된다
• m은 보면 계속 이전의 그라디언트를 참조해주면서 진행한다. 어디서 많이 보지 않았나? 바로 모멘텀이다
  즉, 방향을 조절
• v는 이전의 값들을 참조해주면서 제곱을 통해 현재 변화량이 이전보다 더 높은 영향을 줄 수 있도록 설계하여 스텝에 영향을 준다. 바로 RMSProp이다. 즉, 스텝 조절
• 이렇게 모멘텀과 RMSProp의 조합이 Adam이다

• 이거는 기댓값을 맞춰주기 위한 것
• 그리고 참고로

• 입실론은 무엇일까? 입실론은 굉장히 작은 값을 넣어주는데 파이토치에서 디폴트 값은 $10^{-12}$으로 되어있다
  하는 역할은 만약에 입실론이 없다면 v가 0에 수렴해가는데 0으로 나누게 되므로 값이 갑자기 엄청 커져버릴 수 있는 것이다. 그래서 밑에 그림에서 RMSProp를 보면 끝에가서 갑자기 툭 튀어나가는 것을 확인할 수 있다

• hyperparameter는 각각 $\epsilon = 1^{-8}, \beta_1=0.9, \beta_2=0.999$의 값들이 추천된다

3. Training vs Test vs Validation

• Training이란 학습에 쓰이는 데이터
• Test란 학습을 끝내고 사용될 최종 테스트 데이터
• Validation이란 중간에 테스트를 할 순 없으니 검증할 때 사용하는 데이터

4. 교차 검증 (K-Fold Cross Validation)

• 교차 검증은 트레이닝 데이터가 적어서 일부를 검증 데이터로 사용하기가 곤란한 경우에 사용한다
• 앞에 K는 임의의 숫자이다
• 몇가지 하이퍼 파라미터 세트를 가지고 훈련 데이터와 검증 데이터를 교차해가면서 학습을 진행하고 그 중 val loss 평균이 가장 작은 하이퍼 파라미터 세트를 골라서 훈련 데이터 전체에 대해서 새로 학습시키거나 (1번), 학습해서 나왔던 5개의 모델을 어셈블해서 사용한다 ex) 어셈블 예시 : 다수결

K가 5일 경우 예시

5. DNN, 벡터와 행렬로 표현하기

• 인공신경망을 하나 살펴보자

• 이 그림을 가지고 무언가 계산을 하려면 수식으로 표현해야 한다
• 어떻게 표현할 수 있을까? 행렬과 벡터를 이용해보자

• 여기서 $f_{1}(\left [ x_{1}, x_{2}, x_{3} \right ]) = \left [ f_{1}(x_{1}), f_{1}(x_{2}), f_{1}(x_{3}) \right ]$ 이라고 약속을 하자
• 그러면 다음처럼 표현할 수 있다

• 즉, 인공신경망은 하나의 함수라고 생각할 수 있다

 

 

 

 

 

 

---