표준정규분포,독립or종속변수,결합or주변or조건부확률

 

 

• 오랜만에 수학 공부를 할려니 머리가 안돌아간다...
• 그리고 생각보다 강의 4개를 듣고 포스팅을 하는게 시간이 많이 걸린다...
• 다른 것도 할게 많은데... (AWS, 쿠버네티스, 리눅스, CI/CD...😶)
• 리소스를 너무 많이 사용하는 것 같다는 생각이 들기도 하고...
• 첫날부터ㅋ
• 그래도 일단 될 때까지 해보자 (죽기야 하겄어?)

뿌에엥

 

 

---

 

 

1. 표준 정규 분포 (Standard Normal Distribution)

• 평균이 0이고 분산이 1인 표준화된 정규 분포다
• 표준 정규 분포로 데이터들을 정규화시키면 딥러닝 모델 학습을 시킬 때 더욱 효과적으로 할 수 있고 수식을 계산할 때도 보다 쉽게 계산할 수 있다는 장점이 있다

• 확률 변수 𝑋가 ((𝑋\sim𝑁 (𝜇, 𝜎^2))) 을 따를 때, 다음의 공식으로 표준화를 할 수 있다.
  ((Z=))((X-\mu\over\sigma))
• 그렇다면 확률 변수 Z가 평균이 0이고 분산이 1인 정규분포를 따른다고 할 때 Z는 표준정규분포를 따른다고 한다.
  ((Z\sim N(0,1)))
  확률 변수 Z의 확률밀도함수는 다음과 같다 (단순히 정규분포의 PDF에서 유도)
  ((f(Z)=))((1\over\sqrt{2\pi}))((e^{-{{1\over2}z^2}}))
  
  

정규분포 PDF

• 표준 정규 분포의 확률은 이미 계산이 되어있기 때문에 그래프를 통해 참고하면서 사용하면 좋다. 물론 다른 데이터를 정규화하여 확률을 적용시킬 때는 정확한 값은 아니고 근사값이다.
• 표준 정규 분포의 경우 𝜎의 값이 1이므로, 𝑃 (𝑍 ≤ 1) 을 약 84.1%로 볼 수 있다

Z	+0.00	+0.05
0.0	0.50000	0.51994
0.2	0.57926	0.59871
0.5	0.69146	0.70884
0.7	0.75804	0.77337
0.8	0.78814	0.80234
1.0	0.84134	0.85314
1.5	0.93319	0.93943
2.0	0.97725	0.97982
2.5	0.99379	0.99461
3.0	0.99865	0.99886

1-1. 정규분포 계산 예시

• 보통 IQ를 판단할 때, 평균은 100 표준편차는 ((\sigma))로 설정을 한다.
• IQ가 148이라면 상위 몇 %에 해당하는지 계산해보자
• 확률변수 X가 ((X\sim N(100,24^2)))일 때, X가 148 이상일 확률은
  ((P(X>148)=))$P\left(\frac{X-\mu}{\sigma}> \frac{148-\mu}{\sigma} \right)$=$P\left(Z>\frac{148-\mu}{\sigma}\right)$=$P\left(Z>\frac{148-100}{24}\right)$=$P(Z>2)=1-f_{z}(2)=1-0.97725=0.02275$
  (((Z=))((X-\mu\over\sigma))이니까 그리고 Z가 2일 때는 위 표에 의해 0.97725)
• 즉, IQ 148은 상위 2퍼센트이다

1-2. 정규분포를 이용한 딥러닝 분야의 입력 정규화(Input Normalization)

• 확률 변수 𝑋가 ((𝑋\sim𝑁 (𝜇, 𝜎^2))) 을 따를 때, ((Z=))((X-\mu\over\sigma))이므로
• 입력 데이터가 N(0,1) 분포를 따르도록 표준화하는 예제는 다음과 같다

import matplotlib.pyplot as plt

x1 = np.asarray([33, 72, 40, 104, 52, 56, 89, 24, 52, 73])
x2 = np.asarray([9, 8, 7, 10, 5, 8, 7, 9, 8, 7])

normalized_x1 = (x1 - np.mean(x1)) / np.std(x1)
normalized_x2 = (x2 - np.mean(x2)) / np.std(x2)

plt.axvline(x=0, color='gray')
plt.axhline(y=0, color='gray')
plt.scatter(normalized_x1, normalized_x2, color='black')
plt.show()

평균(mean) = 0, 분산(variance) = 1

• 이런식으로 정규화를 진행하면 여러 데이터셋이 동일한 범위 내의 값을 가지도록 만들 수 있다.

2. 독립 변수(Independent Variable)와 종속 변수(Dependent Variable)

• 독립 변수란 다른 변수에 의해 영향을 받지 않는 변수를 말한다.
• 종속 변수란 독립 변수에 의해 영향을 받아 변화하는 변수를 말한다.
• 논문마다 다른 단어로 표현될 수 있다.

• 딥러닝 모델에서 이미지에 따라 모델의 추론 결과가 달라질 수 있다.
• 즉, 이미지 분류 모델이 독립 변수에 해당하고, 추론 결과가 종속 변수라고 할 수 있다

2-1. 변수와 변량

• 변수(variable)는 독립변수 𝑋를 의미한다

단변수(Univariable)	다변수(Multivariable)
독립 변수가 1개일 때	독립 변수가 여러 개일 때

• 변량(variate)은 종속변수 𝑌를 의미한다

단변량(Univariate)	다변량(Multivariate)
종속 변수가 1개일 때	종속 변수가 여러 개일 때

• 노동 시간, 종업원의 수, 가게의 크기에 따라서 매출액을 예상할 수 있다고 할 때,
  현재 예시에서는 독립 변수가 3개이고, 종속 변수가 1개라고 할 수 있다

3. 결합 확률과 주변 확률

3-1. 독립(Independent)과 종속(Dependent), 그리고 배반 사건

• 독립 (Independent)
  • 𝑃(𝑋 ∩ 𝑌) = 𝑃(𝑋)𝑃(𝑌) 인 경우, 두 사건 𝑋와 𝑌는 서로 독립이다. (필요충분조건)
  • 두 변수가 서로 영향을 주지 않는다는 의미다
• 종속 (Dependent)
  • 한 사건의 결과가 다른 사건에 영향을 줄 때 𝑋와 𝑌를 종속 사건이라고 한다.
• 배반 사건은 “교집합이 없는“ 사건을 의미한다 → 서로 공존할 수 없는 형태
  예시) 
  나의 수학 성적이 50점 이상인 사건과 나의 수학 성적이 50점 미만인 사건

3-2. 배반 vs 독립

	배반 사건	독립 사건
정의	𝑋 ∩ 𝑌 = 𝜙	𝑃(𝑌|𝑋) = 𝑃(𝑌)
의미	두 사건이 동시에 일어나지 않는다	두 사건이 동시에 일어날 때 서로 영향을 주지 않는다
판단 방법	𝑋 ∩ 𝑌 = 𝜙라면, 두 사건은 서로 배반 사건	𝑃(𝑋 ∩ 𝑌) = 𝑃(𝑋)𝑃(𝑌) 라면, 두 사건은 서로 독립 사건

• 𝑃(𝑌|𝑋) = 𝑃(𝑌)라는 것의 의미는 “사건 𝑋의 발생 여부와 상관없이, 사건 𝑌가 발생할 확률은 동일하다.” 라는 뜻이다.

3-3-1. 결합 확률 (Joint Probability)

• 두 개의 사건이 동시에 일어날 확률로, 두 확률 변수의 교집합이 발생할 확률이다.
• 𝑃(𝑋, 𝑌) 혹은 𝑃(𝑋 ∩ 𝑌) 형태로 표현한다

3-3-2. 결합 확률 함수(Joint Probability Function)

• $f_{XY}(x_{i},y_{i})=P(X=x_{i},Y=y_{i})$이다
• 𝑋가 $x_{1}, x_{2},...$의 값을 가질 수 있고, 𝑌가 $y_{1}, y_{2},...$ 의 값을 가질 수 있다고 가정한다
• 결과적으로 단순히 𝑓 𝑥, 𝑦 라고 쓰기도 한다. (𝑋, 𝑌의 결합 확률 분포)
• 𝑋와 𝑌가 가진 범위에서 결합확률함수의 값을 모두 더하면 1이다

3-3-3. 결합확률질량함수 예시

• 이산확률변수가 두 개 이상인 확률질량함수다.
• 확률은 $P_{XY}(x,y)=P(X=x, Y=y)$ 형태로 표현한다
• 또한 이때 $\sum_{i}\sum_{j}P(X=x_{i}, Y=y_{i}) = 1$ 이다. (원소의 총 합은 1이다)
• 테이블의 각 원소를 수학 등급(𝑋)이 𝑥, 영어 등급(𝑌)이 𝑦인 학생의 수라고 해보자

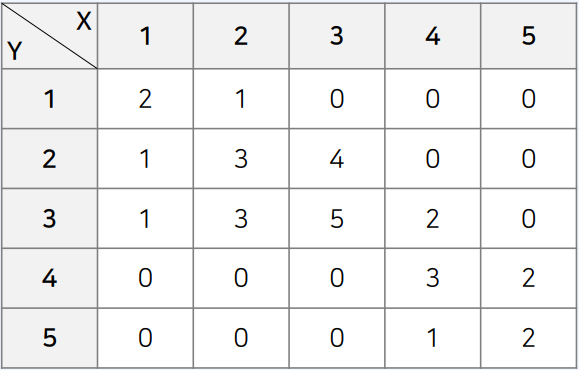
• 다음과 같이 결합 확률 질량 함수로 표현할 수 있다

• 전체 학생 수가 30명일 때, 수학이 1등급이면서 영어가 2등급인 학생이 1명 있다면?
  $P_{XY}(1,2)=P(X=1, Y=2) = \frac{1}{30}$

import pandas as pd


scores = [1, 2, 3, 4, 5]
data = [
    [2, 1, 0, 0, 0],
    [1, 3, 4, 0, 0],
    [1, 3, 5, 2, 0],
    [0, 0, 0, 3, 2],
    [0, 0, 0, 1, 2]
]

# 행(index)과 열(columns) 모두 값으로 [1, 2, 3, 4, 5]를 가진다.
df = pd.DataFrame(data, index=scores, columns=scores)
df.columns.name = "X"
df.index.name = "Y"
pmf = df / df.values.sum()
print(pmf)

import matplotlib.pyplot as plt
import seaborn as sns


sns.set(font_scale=1.5) # 그림(figure)의 기본적인 폰트(font) 크기 설정
plt.rcParams["figure.figsize"] = [10, 8]
# 히트맵(heatmap) 그리기
ax = sns.heatmap(pmf, annot=True,
    xticklabels=[1, 2, 3, 4, 5],
    yticklabels=[1, 2, 3, 4, 5]
)
plt.title("Heatmap", fontsize=20) # 그림(figure)의 제목(title) 설정
plt.show()

3-4-1. 주변확률질량함수 (Marginal Probability Mass Function)

• 두 확률 변수 중에서 하나의 확률 변수에 대해서만 확률 분포를 나타낸 함수다.
• $P_{X}(x)=\sum_{y_{i}}P_{XY}(x,y_{i})$
• $P_{Y}(y)=\sum_{x_{i}}P_{XY}(x_{i},y)$
• 예를 들어 수학이 1등급일 확률은 다음과 같습니다.
• $P_{X}(1)=P_{XY}(1,1) + P_{XY}(1,2) + P_{XY}(1,3) + P_{XY}(1,4) + P_{XY}(1,5)$
• 즉, $X = 1$로 고정하고, 모든 Y 변수에 대하여 확률 값을 더한 것이다
• 이를 모든 𝑋에 대하여 표현하면, 주변 확률 질량 함수가 된다

3-4-2. 주변확률질량함수 예시

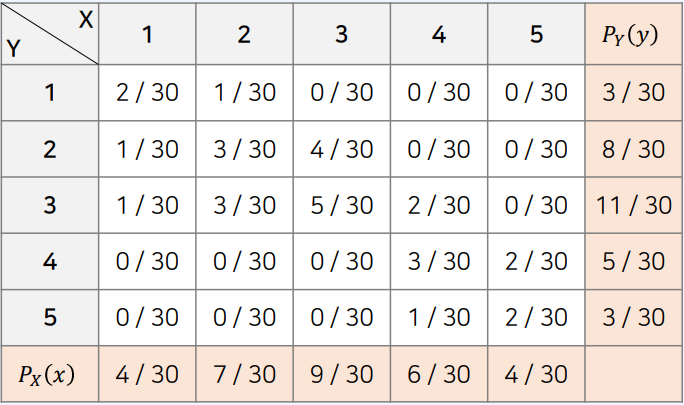
index = 0
x = [0, 1, 2, 3, 4]
plt.bar(x, pmf.iloc[index])
plt.xticks(x, ["1", "2", "3", "4", "5"])
plt.title(f"P(X, Y={index + 1})")
plt.show()

# 각 열마다 합계 계산
marginal_pmf_x = pmf.sum(axis=0)
print(marginal_pmf_x)

# 각 행마다 합계 계산
marginal_pmf_y = pmf.sum(axis=1)
print(marginal_pmf_y)

4. 조건부 확률 (Conditional Probability)

• 어떠한 사건이 일어나는 경우에 다른 사건이 일어날 확률을 의미한다
• 딥러닝 분야에서는 “𝑋 사건이 단서로 주어졌을 때, 𝑌 사건이 발생할 확률”로 이해할 수 있다.
• 𝑥라는 이미지가 입력으로 주어졌을 때, 클래스(class) 𝑦가 나올 확률은 다음과 같이 표현한다
  $P(Y = y \; |\; X = x)$

	스팸 메일	일반 메일	합계
학교 계정	40	30	70
회사 계정	50	60	110
합계	90	90	180

• 하나의 메일을 뽑았을 때, 학교 계정으로 온 메일일 확률
  → 𝑃(학교) = 70/180
• 하나의 메일을 뽑았을 때, 학교 계정으로 온 메일이면서 스팸 메일일 확률 (결합 확률)
  → 𝑃(학교 ∩ 스팸) = 40/180
• 스팸 메일 중 하나를 뽑았을 때, 학교 계정으로 온 메일을 확률 (조건부 확률)
  → 𝑃(학교|스팸) = 40/90

4-1. 조건부 확률 질량 함수

• 조건부 확률 질량 함수 공식:
  $P_{Y|X}(y|x) = \frac{P_{XY}(x,y)}{P_{X}(x)}$
• 영어 성적(𝑌)이 1등급일 때, 수학 성적(𝑋)이 1등급일 확률은?
  → 2 / 3

index = 0
x = [0, 1, 2, 3, 4]
plt.bar(x, pmf.iloc[index] / marginal_pmf_y[index + 1])
plt.xticks(x, ["1", "2", "3", "4", "5"])
plt.title(f"P(X|Y={index + 1})")
plt.show()

 

 

---