확률 분포의 추정, 최대 가능도, 편향, 추세선, 데이터 추출

 

 

 

• 후우... 수식이 너무 많아서 어렵네요...
• 첨 듣는 단어도 너무 많이 나오고, 기호들은 또 왜이렇게 많은지!
• 하지만 처음 하는거니까 익숙하지 않은건 당연한거구 자주 보다보면 익숙해지겠죠?ㅎ

 

---

 

 

 

1. 확률 분포 추정

1-1. 확률 분포 추정이란

• 우리가 가지고 있는 데이터로부터 확률 분포를 추정하는 기술을 의미한다
• 기본적으로 우리가 데이터의 형태를 보고, 원하는 분포로 추정할 수 있다
  • 베르누이 분포: 데이터가 0 혹은 1의 형태
  • 정규 분포: 데이터가 크기 제한이 없는 실수 형태
  • 카테고리 분포: 데이터가 카테고리 값 형태
• 주어진 데이터를 이용해 확률 분포를 계산하는 대표적인 두 가지 방법이 존재한다
  1. 모멘트 방법
  2. 최대 가능도 추정

1-2. 모멘트 방법 (Method of Moment)

• 확률분포에서 계산한 특징 값의 일종으로, 𝑛차 모멘트는 다음과 같이 정의된다

• 1차 모멘트는 평균, 2차 모멘트는 분산에 해당한다
• 1차부터 무한대 차수에 이르기까지 두 확률 분포의 모든 모멘트 값이 같다면 두 확률 분포는 같다고 할 수 있다
  → 즉 확률 분포를 추정했다라고 할 수 있음
• 1차 모멘트는 데이터의 평균(mean)과 같다

• 2차 모멘트는 데이터의 분산(variance)과 같다

1-3. 모멘트 방법을 활용한 정규 분포 추정

• 모멘트 방법을 이용해 정규 분포의 𝑝𝑎𝑟𝑎𝑚𝑒𝑡𝑒𝑟를 추정할 수 있다

등급	1등급	2등급	3등급	4등급	5등급	6등급	7등급	합계
학생 수	3	5	7	10	6	6	3	40

• 정규 분포의 함수에서 평균(𝜇)과 표준편차(𝜎)를 넣어 확률 값을 계산할 수 있다

• 이 공식을 통해 주어진 데이터들로부터 확률 분포를 추정해내고 그래프로 그릴 수 있다

import math

arr = [1] * 3 + [2] * 5 + [3] * 7 + [4] * 10 + [5] * 6 + [6] * 6 + [7] * 3

# 평균(mean) 계산
mean = 0
for x in arr:
    mean += x / len(arr)

# 분산(variance) 계산
variance = 0
for x in arr:
    variance += ((x - mean) ** 2) / len(arr)

# 표준 편차(standard deviation) 계산
std = math.sqrt(variance)

print(f"평균: {mean:.3f}")
print(f"분산: {variance:.3f}")
print(f"표준 편차: {std:.3f}")

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = [10, 8]
x = np.linspace(mean - 10, mean + 10, 1000) # 평균(mean)을 중심으로 다수의 x 데이터 생성
# 정규 분포의 확률 밀도 함수(probability density function)
y = (1 / (np.sqrt(2 * np.pi) * std)) * np.exp(-1 / (2 * (std ** 2)) * ((x - mean) ** 2))
plt.plot(x, y)
plt.xlabel("$x$")
plt.ylabel("$f_X(x)$")
plt.show()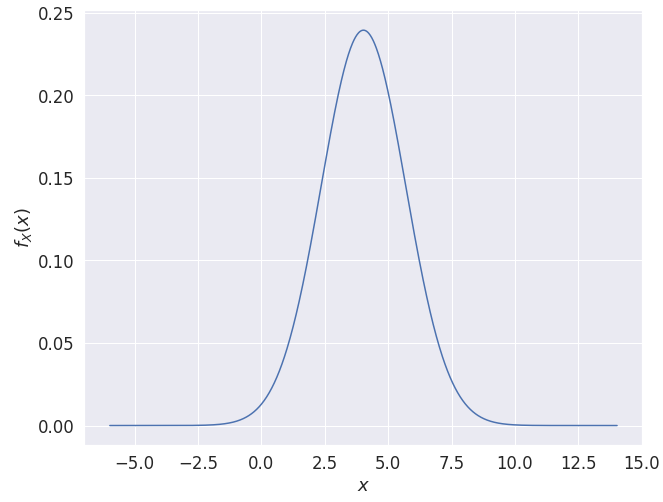

1-4. 최대 가능도 추정 (Maximum Likelihood Estimation)

• 이론적으로(수식적으로) 가장 가능성이 높은 모수(parameter)를 찾는 방법이다
• 기본적으로 모든 추정 방법 중에서 가장 널리 사용되는 방법 중 하나다
• 확률 분포 𝑋에 대한 확률 함수를 다음과 같이 표현할 때
  (단, x는 확률 분포가 가질 수 있는 실수 형태의 값이고, 𝜃와 𝑥 모두 스칼라이거나 벡터이다)
  𝑝(𝑥;𝜃)
  가지고 있는(관측된) 데이터 𝑥를 토대로 모수 𝜃를 찾아야 하므로 모수를 변수로 간주하는 것이다
  가능도 함수 : 𝐿(𝜃;𝑥) = 𝑝(𝑥;𝜃)
  라고 표현할 수 있다
• 추정하고자 하는 확률 분포에 따라 가능도 함수를 다르게 정의할 수 있다
  1. 베르누이 확률 분포를 추정하는 경우
     • 𝜃 = 𝜇
  2. 정규 분포를 추정하는 경우
     • $\theta = (\mu,\sigma^{2})$
• 최대 가능도 추정은 다음과 같은 문제를 해결하는 것이 목표다

Hat 기호는 예측된 변수를 의미

• 가지고 있는 정보를 토대로, 가능도(likelihood)를 최대로 만드는 𝑝𝑎𝑟𝑎𝑚𝑒𝑡𝑒𝑟를 찾는 것을 표현

1-5. 정규 분포의 최대 가능도 추정

• 일단 정규분포의 확률밀도함수는 다음과 같다. (𝜇와 𝜎가 상수로 주어진 상황)
  → 모수를 알고 있으며, 적분했을 때 면적은 항상 1이다

• 가능도 함수는 다음과 같다. (𝑥가 상수로 주어진 상황)
→ 데이터 𝑥를 알고 있으며, 적분했을 때 면적은 1이 아닐 수 있다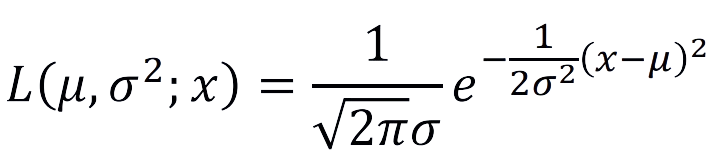

• 그리고 N개의 데이터가 있을 때 가능도 함수를 봐보자
• 각 표본 데이터는 같은 확률 분포에서 나온 독립적인 값이므로 N개의 데이터가 나올 확률 밀도 함수는 각각의 확률을 서로 곱해준 것과 같게 되므로 다음과 같이 표현할 수 있다

• 위의 두가지를 사용하면, 정규 분포의 최대 가능도 함수를 다음과 같이 정리할 수 있다

• 여기서 가능도 값을 최대로 하는 모수를 구하는 것이 목표이므로
• 𝜇와 $\sigma^{2}$로 미분한 값이 0일 때, 가능도(likelihood) 값이 최대

• 식을 전개하면, 해는 다음과 같다

• 정규 분포의 평균(𝜇)은 표본 평균과 같고, 분산(𝜎 2 )은 표본 분산과 같다는 것을 알 수 있다

2. 편향과 오차

2-1. 편향 (Bias)

• 편향된 데이터(biased data): 실제 데이터를 반영하지 못하고, 편향된 데이터를 의미한다

2-2. 편향(Bias)과 분산(Variance)

• 편향(bias)이 높을 때: 모델이 예측한 값이 정답과 멀리 떨어져 있는 경우
• 분산(variance)이 높을 때: 모델이 예측한 값이 서로 멀리 떨어져 있는 경우

2-3. 오차 (Error)

• 오차 : 실제 정답과 우리 모델이 예측한 값의 차이
• 오차는 내 모델이 얼마나 잘못되었는지 알려주는 수치화된 값으로 이해할 수 있다
• 비용(cost) 혹은 손실(loss)이라고도 부른다

2-4. 평균 제곱 오차 (Mean Squared Error)

• 대표적인 오차 계산 함수 중 하나가 평균 제곱 오차(mean squared error)다
• 평균 제곱 오차는 말 그대로 오차(error)를 제곱한 값의 평균을 의미한다
• 각 데이터가 (입력 𝑥, 정답 𝑦)로 구성될 때, MSE(Mean Squared Error) 공식은 다음과 같다

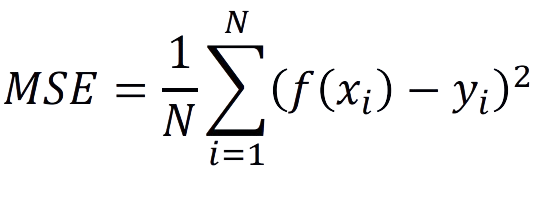
• 예를 들어 실제 나이가 27세(y=27)인 사람의 얼굴 이미지 x가 주어졌을 때, 모델의 예측 결과가 29세라면, 제곱 오차는 $(29-27)^{2}=4$이다

3. 최소 제곱법과 추세선

3-1. 최소제곱법 (Least Square Method)

• 평균 제곱 오차(mean squared error)를 이용할 수 있다
• 모든 데이터에 대한 $(\mbox{실제 값 - 예상 값})^{2}$의 합으로 비용을 계산한다
• 따라서 다음 식을 최소화하는 파라미터 (𝑊, 𝑏)를 찾는 것이 목표다
  → 이를 최소제곱법이라고 한다

3-2. 선형 함수에서 비용(cost) 구하기 예시

• 가설 함수: 𝑓(𝑥) = 𝑊𝑥 + 𝑏

• 𝑊 = 1, 𝑏 = 2일 때의 비용을 계산해 보자.
• 𝑦 = 𝑥 + 2

• 비용을 더 줄이려면, 𝑊와 𝑏를 어떻게 바꾸어야 할까

3-2-1. 최소 제곱 값을 얻는 방법 – 경사 하강

• 최소 제곱을 얻는 방법 중 하나는 바로 “경사 하강”을 이용하는 것이다
• 경사 하강(gradient descent): 기울기를 이용하여 비용을 줄이는 방법이다
• 미분을 이용하면 특정 값에서의 기울기를 구할 수 있다
• 기울기가 최소가 되는 지점을 찾는 것!

3-3. 최소제곱법으로 추세선 찾기

• 다시 말해, 비용을 줄이기 위한 방법은 다음과 같다
  → 비용 함수를 가중치(𝑊)로 미분해 기울기를 구한 뒤에, 기울기의 반대 방향으로 𝑊를 업데이트
• 어느 정도의 크기로 이동해야 할까?
• 적절한 크기로 이동할 수 있도록, 학습률(learning rate)을 곱하여 이동한다
• 예를 들어 학습률이 0.01이고, 기울기가 7이라면? 
• 𝑊 ← 𝑊 − 7 ∗ 0.01로 업데이트한다
• 학습 과정을 반복하면, 가중치는 올바른 지점으로 수렴할 수 있다

4. 데이터 추출 (Data Sampling)

• 기계 학습 분야에서는 데이터를 랜덤으로 추출하는 경우가 많다
• 파이썬을 이용하면 간단하게 데이터 추출을 할 수 있다
• 𝑐ℎ𝑜𝑖𝑐𝑒() 메서드를 사용해 리스트 내에서 1개의 원소를 랜덤으로 추출할 수 있다

import random

arr = [1, 2, 3, 4, 5]
sampled = random.choice(arr)
print(sampled)

• 𝑠𝑎𝑚𝑝𝑙𝑒() 메서드를 사용해 𝑘개의 데이터를 중복 없이 추출할 수 있다
• 단, 데이터의 개수를 초과할 수 없다 (아래 예시에서는 5를 초과할 수 없다)

import random

arr = [1, 2, 3, 4, 5]
sampled = random.sample(arr, 3)
print(sampled)

• 리스트 내에서 𝑘개의 데이터를 중복을 허용하여 추출할 수 있다

# 1번 : 반복문 사용
import random

arr = [1, 2, 3, 4, 5]
sampled = [random.choice(arr) for i in range(3)]
print(sampled)

# 2번 : 𝑐ℎ𝑜𝑖𝑐𝑒𝑠() 메서드를 사용
import random

arr = [1, 2, 3, 4, 5]
sampled = random.choices(arr, k=3)
print(sampled)

• 𝑐ℎ𝑜𝑖𝑐𝑒𝑠() 메서드는 중복을 허용하기 때문에, 𝑘가 원소의 개수보다 클 수 있다

import random

arr = [1, 2, 3, 4, 5]
# 중복을 허용하기 때문에, k가 원소의 개수보다 클 수 있다.
sampled = random.choices(arr, k=7)
print(sampled)

• 균등 분포(Uniform Distribution)에서 추출

import numpy as np

sampled = np.random.uniform(0, 1, 5)
print(sampled)
# [0.071 0.375 0.029 0.341 0.637]

 

• 표준 정규 분포(평균: 0, 표준편차: 1)에서 5개의 데이터를 추출한다.

import numpy as np

sampled = np.random.normal(0, 1, 5)
print(sampled)
# [ 0.167 -0.129 -0.432 -0.592  1.545]

 

 

 

---