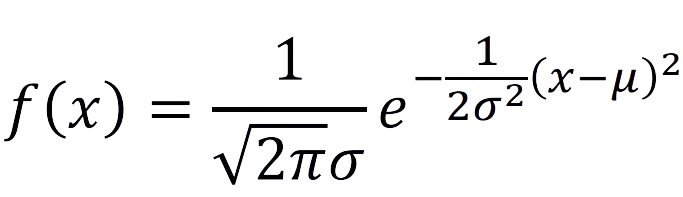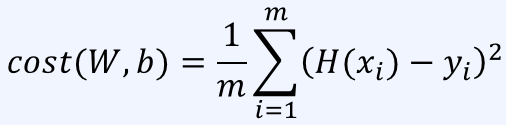전체 글 (134)
방명록
- 샘플링, 추세선 그리기, 통계 실습2024년 02월 19일 05시 32분 22초에 업로드 된 글입니다.작성자: 재형이반응형
- 실습 위주로 ㄱㄱ
1. 다양한 분포에서 샘플링(Sampling) 해보기
- 샘플링이란 어떤 자료에서 일부 값을 추출하는 것을 의미한다
- 파이썬의 numpy를 사용하면 간단하게 정규 분포, 베타 분포 등에서 샘플링을 진행할 수 있다
import numpy as np import matplotlib.pyplot as plt1-1. NumPy 균등 분포(Uniform Distribution)
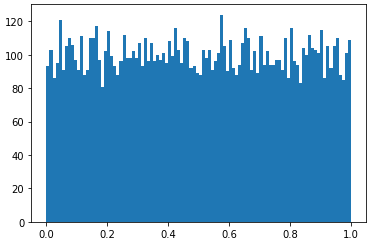
- 구간 내 모든 데이터에 대하여 추출 확률이 동일한 분포이다
sampled = np.random.uniform(low=0.0, high=1.0, size=(2, 4)) print(sampled)
- 이런 식으로 균등 분포를 가지는 데이터를 가져올 수 있다
- 추출한 데이터는 히스토그램(histogram)을 그려 확률 분포를 시각화할 수 있다
sampled = np.random.uniform(low=0.0, high=1.0, size=10000) cnt, bins, ignored = plt.hist(x=sampled, bins=100) plt.show()
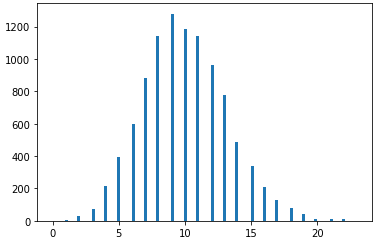
1-2. NumPy 이항 분포(Binomial Distribution)
- 이항 분포도 Numpy를 통해서 데이터를 뽑아오고 히스토그램을 그려서 시각화해보자
n = 10 p = 0.5 sampled = np.random.binomial(n, p, 10000) cnt, bins, ignored = plt.hist(x=sampled, bins=10, density=True) plt.show()
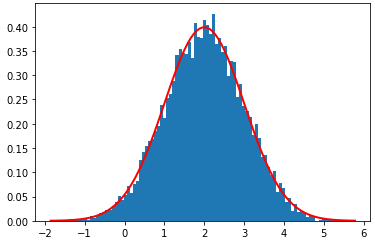
1-3. NumPy 정규 분포(Normal Distribution)

- 정규 분포 공식을 사용하여 추세선도 그려볼 수 있다
def pdf(x): return 1 / (np.sqrt(2 * np.pi) * sigma) * np.exp(-(x - mu) ** 2 / (2 * sigma ** 2)) mu = 2 # mean sigma = 1 # standard deviation sampled = np.random.normal(mu, sigma, 10000) cnt, bins, ingored = plt.hist(sampled, 100, density=True) plt.plot(bins, pdf(bins), linewidth=2, color='r') plt.show()
1-4. NumPy 포아송(Poisson) Distribution
- 일정한 시간 내 발생하는 사건의 발생 횟수에 대한 확률을 계산한다
- lam : 단위 시간당 발생 횟수
lam = 10 sampled = np.random.poisson(lam, 10000) cnt, bins, ingored = plt.hist(sampled, 100) plt.show()
1-5. NumPy 지수 분포(Exponential Distribution)
- 특정 시점에서 어떤 사건이 일어날 때까지 걸리는 시간의 확률을 계산할 때 사용한다
lam = 2 beta = 1 / lam sampled = np.random.exponential(beta, 10000) cnt, bins, ingored = plt.hist(sampled, 100, density=True) plt.show()
2. 입력 정규화
2-1. 통계적 특성 분석화하기
- 딥러닝에서는 모델의 입력으로 데이터를 넣을 때, 사전에 전처리 과정을 거친다
- 특히 입력 정규화(input normalization)는 현대 딥러닝 모델의 학습에 있어서 사용 빈도가 매우 높다
- 이를 위해 이미지의 평균(mean), 표준 편차(standard deviation)을 계산해야 하는 경우가 많다
- 데이터 세트가 주어졌을 때, 통계적인 값을 계산해 보자
2-2. 이미지 정규화(Image Normalization)
- 색상 이미지의 R, G, B 채널(channel) 각각에 대하여 평균을 0으로, 표준 편차를 1로 맞추어 주는 작업을 말한다
- 내가 가지고 있는 데이터 세트가 N(0,1) 분포를 따르게 된다
- 입력 데이터를 정규화하여 학습 속도(training speed)를 개선할 수 있다
- 각각의 픽셀(pixel) 혹은 특징(feature)이 비슷한 값의 범위를 가지게 된다
- 이는 기울기(gradient) 값을 적절히 조절(control)할 수 있게 도와준다
- CIFAR-10은 32 X 32 X 3의 해상도의 사물 데이터를 모아 놓은 데이터 세트다
- CIFAR-10 데이터 세트는 비행기(airplane), 자동차(automobile), 새(bird), 고양이(cat) 등 총 10개의 클래스로 구성된다
- 학습 데이터는 50,000개이고, 테스트 데이터는 10,000개다
import torch import torchvision.datasets as datasets from torchvision import transforms import numpy as np import matplotlib.pyplot as plt # CIFAR-10 데이터 세트 불러오기 train_dataset = datasets.CIFAR10( root="./data", train=True, download=True, transform=transforms.ToTensor() ) # 모든 이미지를 하나씩 확인하기 imgs = [] labels = [] for data in train_dataset: img, label = data imgs.append(img) labels.append(label) print(f"The number of images: {len(imgs)}") print(f"The number of labels: {len(labels)}") print(f"The shape of an image: {imgs[0].shape}") # 전체 데이터 세트를 NumPy 배열로 변환 numpy_imgs = torch.stack(imgs, dim=0).numpy() print(f"The shape of the NumPy data array: {numpy_imgs.shape}") # calculate mean over each channel (r, g, b) mean_r = numpy_imgs[:,0,:,:].mean() mean_g = numpy_imgs[:,1,:,:].mean() mean_b = numpy_imgs[:,2,:,:].mean() print(f"The mean of R: {mean_r}") print(f"The mean of G: {mean_g}") print(f"The mean of B: {mean_b}") # calculate standard deviation over each channel (r, g, b) std_r = numpy_imgs[:,0,:,:].std() std_g = numpy_imgs[:,1,:,:].std() std_b = numpy_imgs[:,2,:,:].std() print(f"The std of R: {std_r}") print(f"The std of G: {std_g}") print(f"The std of B: {std_b}") def get_statistics(dataset): # 모든 이미지를 하나씩 확인하기 imgs = [] labels = [] for data in dataset: img, label = data imgs.append(img) labels.append(label) # 전체 데이터 세트를 NumPy 배열로 변환 numpy_imgs = torch.stack(imgs, dim=0).numpy() print(f"The shape of the NumPy data array: {numpy_imgs.shape}") # 회색(grayscale) 이미지인 경우 if numpy_imgs.shape[1] == 1: return numpy_imgs[:,0,:,:].mean(), numpy_imgs[:,0,:,:].std() # calculate mean over each channel (r, g, b) mean_r = numpy_imgs[:,0,:,:].mean() mean_g = numpy_imgs[:,1,:,:].mean() mean_b = numpy_imgs[:,2,:,:].mean() # calculate standard deviation over each channel (r, g, b) std_r = numpy_imgs[:,0,:,:].std() std_g = numpy_imgs[:,1,:,:].std() std_b = numpy_imgs[:,2,:,:].std() return (mean_r, mean_g, mean_b), (std_r, std_g, std_b) def imshow(img, grayscale=False): npimg = img.numpy() if grayscale: # (높이, 너비, 채널) 형태로 변환 npimg = np.transpose(npimg, (1, 2, 0)) # 흑백 이미지는 채널 차원 제거 npimg = np.squeeze(npimg) plt.imshow(npimg, cmap="gray") else: # (높이, 너비, 채널) 형태로 변환 npimg = np.transpose(npimg, (1, 2, 0)) plt.imshow(npimg, cmap="gray") plt.show() dataset = datasets.CIFAR10( root="./data", train=True, download=True, transform=transforms.ToTensor() ) img, label = dataset[0] print(f"Image example: {img.shape}") imshow(img, grayscale=False) (mean_r, mean_g, mean_b), (std_r, std_g, std_b) = get_statistics(dataset) print(f"The mean of R: {mean_r}") print(f"The mean of G: {mean_g}") print(f"The mean of B: {mean_b}") print(f"The std of R: {std_r}") print(f"The std of G: {std_g}") print(f"The std of B: {std_b}")
이상한 그림 아니다... 화질이 안좋아서 그런거임ㅇㅇ
3. 추세선 그리기
- 특정한 데이터 사례가 주어졌을 때, 추세선(trend line)을 그려보고 특성을 분석할 수 있다
- 추세선은 다항 함수 형태로 표현할 수 있다
- 하지만, 일반적으로 1차 함수 직선 형태가 가장 많이 사용된다
- 한 장사꾼의 매출의 추세선을 그려서 노동 시간에 따른 매출을 예측해보자

- 7시간을 일 했을 때 매출은 얼마일까?
- 9시간을 일 했을 때 매출은 얼마일까?
- 입력(노동 시간)과 출력(매출)이 선형 함수(일차 함수) 형태를 가진다
- 가설 함수: f(x)=Wx+b
- W와 b를 수정해 나가면서 가장 합리적인 식을 찾아낼 수 있다
- 예를 들어 현재의 W 가 10,000이고, b 가 5,000이라고 해보자
import matplotlib.pyplot as plt import numpy as np from sklearn import datasets, linear_model from sklearn.metrics import mean_squared_error X = [1, 2, 3, 4, 5, 6, 8] y = [25000, 55000, 75000, 110000, 128000, 155000, 210000] class F(): def __init__(self, W, b): self.W = W self.b = b def forward(self, x): prediction = self.W * x + b return prediction W = 10000 b = 5000 model = F(W, b) print(f"5시간 일했을 때 매출: {model.forward(5)}원")
- 현재 우리의 모델이 있을 때, 모델이 얼마나 잘못되었는지 평가하는 방법이 필요하다
- 비용(cost): 우리의 모델이 뱉은 답이 실제 정답과 얼마나 다른지 수치화한 것
- 선형 회귀 문제에서는 평균 제곱 오차(mean squared error)를 이용할 수 있다
- 모든 데이터에 대한 실제 값에서 예상 값을 뺀 것의 제곱의 합으로 비용을 계산한다
- 따라서 다음 식을 최소화하는 파라미터 ( W , b )를 찾는 것이 목표다

- 이를 최소제곱법(minimum squared method)라고도 한다
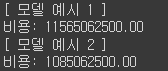
import matplotlib.pyplot as plt import numpy as np from sklearn import datasets, linear_model from sklearn.metrics import mean_squared_error X = [1, 2, 3, 4, 5, 6, 8] y = [25000, 55000, 75000, 110000, 128000, 155000, 210000] class F(): def __init__(self, W, b): self.W = W self.b = b def forward(self, x): prediction = self.W * x + b return prediction def cost(prediction, y): result = 0 for i in range(len(prediction)): result += (prediction[i] - y[i]) ** 2 return result / len(prediction) X_train = [1, 2, 3, 4, 5, 6, 8] y_train = [25000, 55000, 75000, 110000, 128000, 155000, 210000] X_test = [4.5, 6.5, 7, 9] y_test = [117000, 182000, 190000, 221500] print("[ 모델 예시 1 ]") W = 10000 b = 5000 model = F(W, b) prediction = [model.forward(x) for x in X_test] print(f"비용: {cost(prediction, y_test):.2f}") print("[ 모델 예시 2 ]") W = 30000 b = 5000 model = F(W, b) prediction = [model.forward(x) for x in X_test] print(f"비용: {cost(prediction, y_test):.2f}")
- 사이킷런의 선형 회귀(linear regression) 라이브러리를 이용해 1차 함수 형태의 추세선을 그릴 수 있다
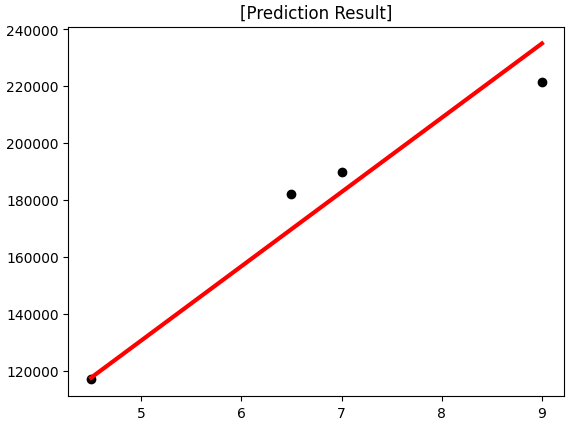
X_train = [[1], [2], [3], [4], [5], [6], [8]] y_train = [25000, 55000, 75000, 110000, 128000, 155000, 210000] X_test = [[4.5], [6.5], [7], [9]] y_test = [117000, 182000, 190000, 221500] # 선형 회귀(linear regression) 모델 학습 수행 regressor = linear_model.LinearRegression() regressor.fit(X_train, y_train) # 학습 결과 출력 print(f"Coefficients: {regressor.coef_}") print(f"Bias: {regressor.intercept_}") y_pred = regressor.predict(X_test) print(f"예측 결과: {y_pred}") print(f"MSE (Mean Squared Error): {mean_squared_error(y_test, y_pred)}")
plt.title("[Prediction Result]") plt.scatter(X_test, y_test, color="black") plt.plot(X_test, y_pred, color="red", linewidth=3) plt.show()
반응형'인공지능 > 확률과 통계' 카테고리의 다른 글
확률 분포의 추정, 최대 가능도, 편향, 추세선, 데이터 추출 (4) 2024.02.04 베이즈 정리, 평균과 기댓값, 분산과 표준편차, 공분산 (0) 2024.02.03 표준정규분포,독립or종속변수,결합or주변or조건부확률 (6) 2024.02.02 확률 개요 및 이산 확률 분포, 연속확률분포 (0) 2024.02.01 다음글이 없습니다.이전글이 없습니다.댓글재형이의 성장통 일지하루 하루 성장하자